每年六月,法国高中生都会迎来他们人生中最重要的考试之一——Baccalauréat(法国高中毕业会考)。对于选择“数学专选(Spécialité Mathématiques)”的学生来说,这场长达 4 小时的笔试,不仅是检验知识的终点,更是通往大学的门票。
这篇文章中,我们特别整理并呈现了:
🔹2025 年法国高中数学专选科目全国统考(Métropole – Jour 1)原题全文
🔹官方权威答案与解析(由法国数学教师团队编写)
🔹逐题中文翻译(力求准确、自然、便于中国学生理解)
📖适合阅读人群:
✅ 想要了解法国数学教育风格的同学
✅ 有意申请法国大学预科/工程师学校/高商项目的学生
✅ 准备数学竞赛、A-Level、IB、法语TCF的跨文化学习者
✅ 教师、翻译者、出题人等教育行业从业者
🧠这不仅是一份考试卷,更是一扇窗:
透过一张试卷,你将看到法国高中数学是如何在建模、逻辑推演、函数分析、几何与统计等维度,融合现实与抽象、计算与思辨的。
希望这份双语材料,能成为你学习、教学或研究中的一份参考与灵感。
原试卷:





 以下是原题翻译:
以下是原题翻译:
2025年法国高中毕业会考数学专业第一场试题
2025年法国高中毕业会考(数学专业)第一场 - 大陆地区考试时间:2025年6月17日(星期二)考试时长:4小时允许使用带有考试模式的计算器或无记忆(中学型)计算器
第一题(5分)
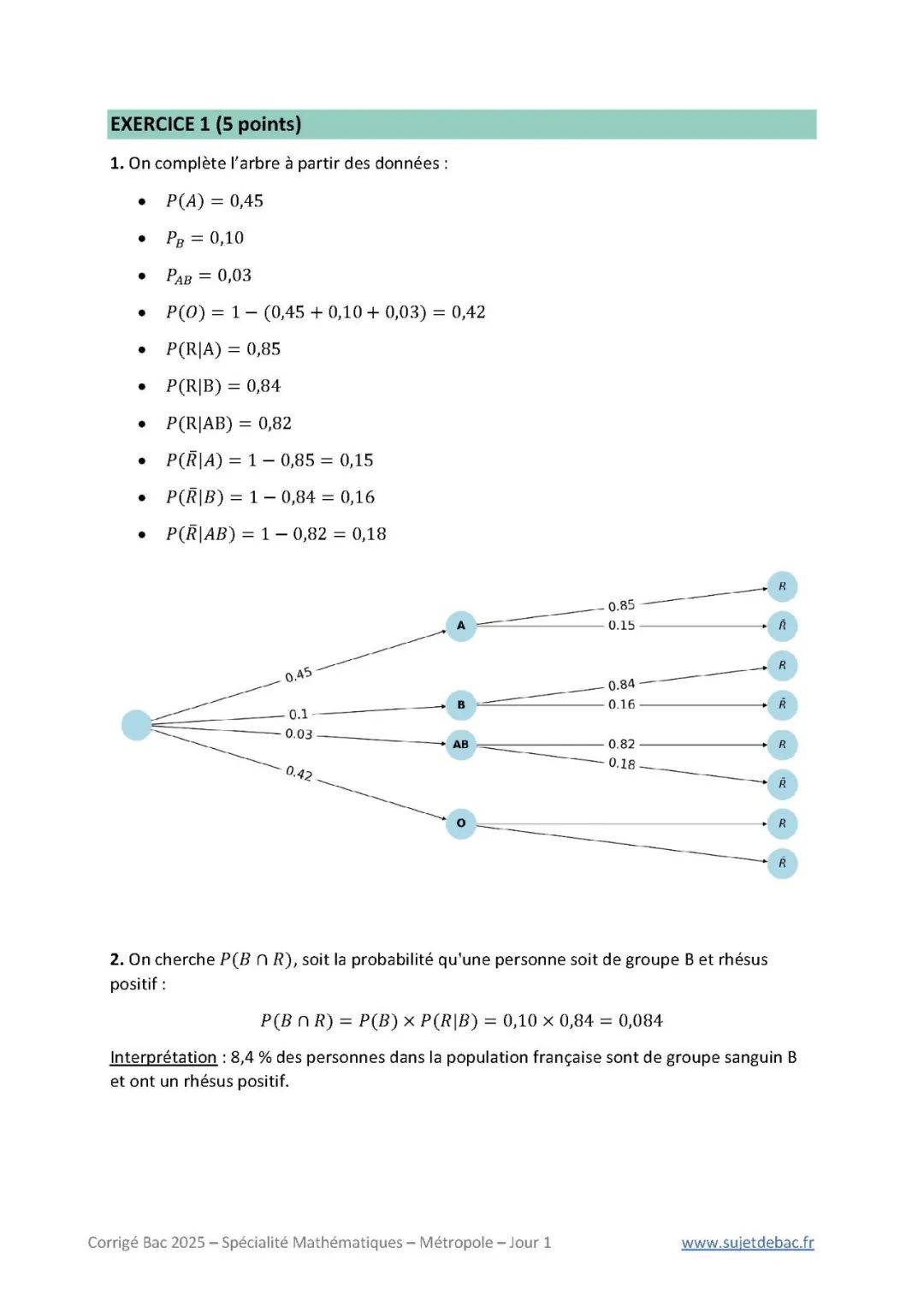
人类共有四种血型:A型、B型、AB型和O型。每种血型都可能具有Rh因子。如果该因子存在,我们称其为Rh阳性;否则为Rh阴性。在法国人口中:- 45%为A型,其中85%为Rh阳性;- 10%为B型,其中84%为Rh阳性;- 3%为AB型,其中82%为Rh阳性。从法国人口中随机抽取一人:1. 补全右侧树状图的10个空白。2. 证明 P(B ∩ R) = 0.084,并在题目情境下解释其含义。3. 已知 P(R) = 0.8397,证明 P_O(R) = 0.83。4. O型Rh阴性是唯一可以给所有人输血的“万能献血者”。证明随机选中一人为万能献血者的概率为0.0714。5. 从某城市选出100人构成样本,X为其中万能献血者人数:a. 说明X服从何种分布并给出其参数; b. 计算X ≤ 7的概率,保留三位小数; c. 计算X的期望和方差,分别精确到两位小数。6. 在N个城市中进行采血,每城采样100人,定义M_N为N城平均万能献血者人数: a. M_N表示什么? b. 计算E(M_N); c. 证明Var(M_N) = 6.63 / N; d. 求使P(7 < M_N < 7.28) ≥ 0.95的最小N值(使用Bienaymé-Tchebychev不等式)。
第二题(6分)
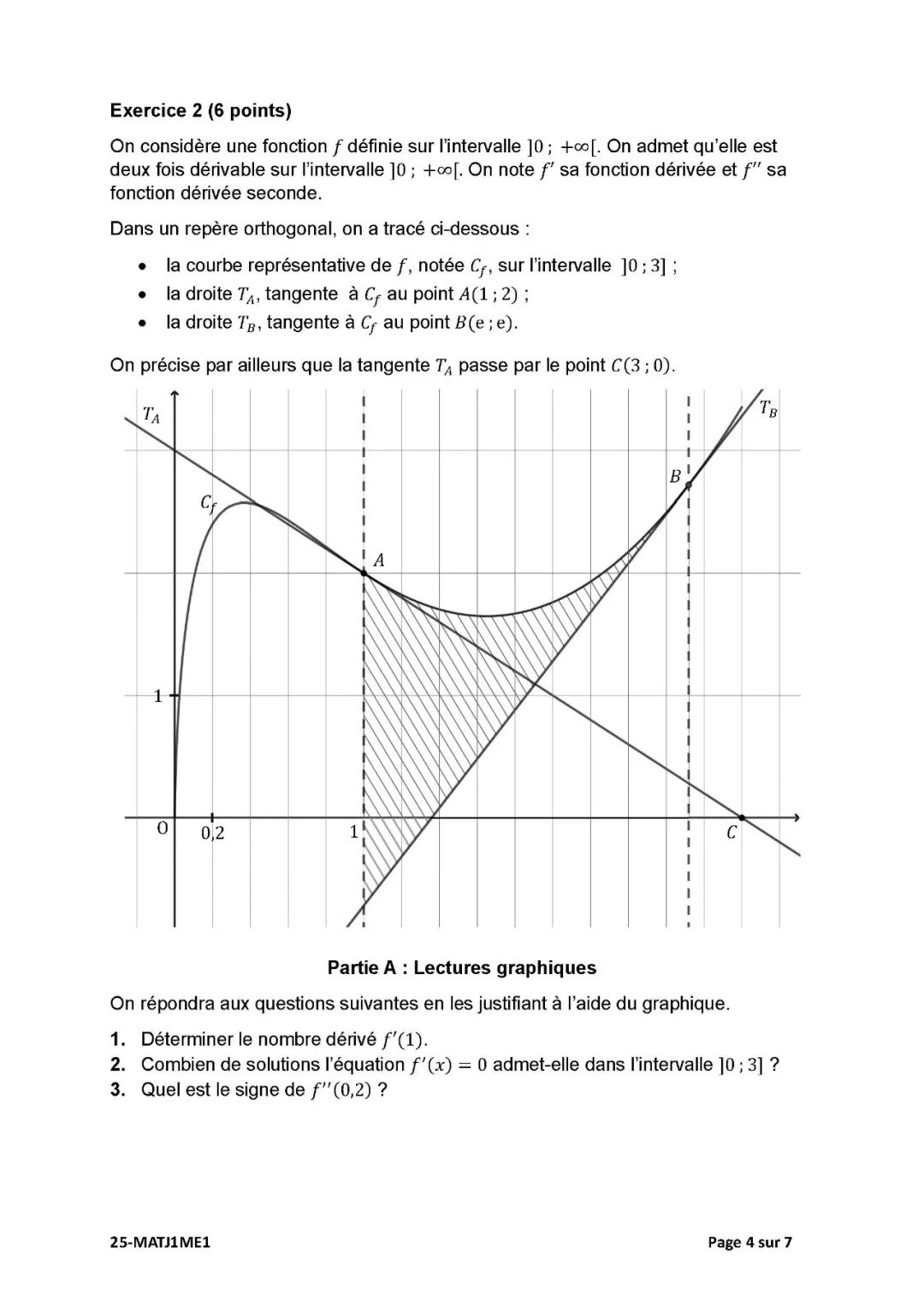
本题研究定义在区间 ]0 ; +∞[ 上的函数 f,它在该区间上二阶可导。在一个正交坐标系中,已绘制:- 函数 f 的图像 C_f,定义域为 ]0 ; 3];- 点 A(1, 2) 处的切线 T_A;- 点 B(e, e) 处的切线 T_B。已知 T_A 经过点 C(3, 0)。A. 图像阅读:1. 由图像判断 f'(1) 的值;2. 在区间 ]0 ; 3] 上,方程 f'(x) = 0 有几个解?3. 判断 f''(0.2) 的符号。B. 函数 f 的研究:函数定义为:f(x) = x[2(ln x)^2 − 3 ln x + 2]。1. 解方程 2X² − 3X + 2 = 0,并据此说明 C_f 不与横轴相交。2. 计算 f(x) 在 +∞ 处的极限;给出在 0 处的极限(已知为 0)。3. 已知导函数 f'(x) = 2(ln x)^2 + ln x − 1:a. 证明 f''(x) = (1/x)(4 ln x + 1); b. 研究 f 的凸性,给出拐点的横坐标; c. 证明在区间 [1 ; +∞[ 上,图像 C_f 位于切线 T_B 上方。C. 面积计算:1. 证明切线 T_B 的方程为 y = 2x − e;2. 通过分部积分,证明:∫[1 到 e] x ln x dx = (e² + 1)/4;3. 已知 ∫[1 到 e] x(ln x)^2 dx = (e² − 1)/4,计算由 C_f、T_B 以及 x=1 和 x=e 所围区域的面积 A。
第三题(4分)
判断以下命题的真假,并提供证明。空间坐标系为正交直角坐标系 (O ; i, j, k):1. 点 A(−1, 0, 5),B(3, 2, −1)- 命题1:直线 AB 的参数方程为:x = 3 − 2t,y = 2 − t,z = −1 + 3t;- 命题2:向量 (5, −2, 1) 是平面 OAB 的法向量。2. 直线 d 的参数方程为:x = 15 + k,y = 8 − k,z = −6 + 2k;直线 d' 的参数方程为:x = 1 + 4s,y = 2 + 4s,z = 1 − 6s;- 命题3:d 与 d' 不共面。3. 平面 P 的方程为 x − y + z + 1 = 0;点 C(2, −1, 2)- 命题4:点 C 到平面 P 的距离为 2√3。
第四题(5分)
研究生物学家研究地中海藻类“海草”(posidonie)在 Porquerolles 岛附近 Alycastre 海湾的覆盖面积。总研究区域面积为 20 公顷,2024年7月1日时藻类覆盖面积为 1 公顷。A. 离散模型研究:记 u_n 为第 n 年(从2024年起)的覆盖面积(单位:公顷),即 u_0 = 1。模型为:u_{n+1} = −0.02 u_n² + 1.3 u_n。1. 计算2025年7月1日的预计覆盖面积。2. 定义函数 h(x) = −0.02x² + 1.3x,x∈[0, 20],并知其在该区间上递增:a. 证明对任意自然数 n,有 1 ≤ u_n ≤ u_{n+1} ≤ 20; b. 推出 u_n 收敛,记极限为 L; c. 证明 L = 15。3. 生物学家想知道何时覆盖面积超过14公顷: a. 无需计算,说明此现象必然发生; b. 补全下列算法以输出所需时间:def seuil(): n=0 u=1 while ………………… : n= ………… u= ………… return nB. 连续模型研究:定义函数 f(t) 为从2024年7月1日开始经过 t 年时的覆盖面积,满足:- f(0) = 1,f 在 [0, +∞[ 上可导且不为0,满足微分方程 y' = 0.02 y(15 − y)1. 定义 g(t) = 1 / f(t),证明其满足 y' = −0.3 y + 0.02;2. 解该微分方程;3. 推导 f(t) = 15 / (14e^(−0.3t) + 1);4. 求 f(t) 在 +∞ 时的极限;5. 解不等式 f(t) > 14 并解释其实际意义。
答案与解析:











以下是答案与解析翻译:
2025年法国高中毕业会考 数学专业 第一场 答案与解析
第一题(5分)解析
1. 根据已知数据补全树状图:- P(A) = 0.45,P(B) = 0.10,P(AB) = 0.03,P(O) = 1 - (0.45 + 0.10 + 0.03) = 0.42 - P(R|A) = 0.85 → P(R̄|A) = 0.15 - P(R|B) = 0.84 → P(R̄|B) = 0.16 - P(R|AB) = 0.82 → P(R̄|AB) = 0.182. 计算P(B ∩ R): P(B ∩ R) = P(B) × P(R|B) = 0.10 × 0.84 = 0.084。 解释:约8.4%的法国人口为B型且Rh阳性。3. 利用全概率公式: P(R) = P(A∩R) + P(B∩R) + P(AB∩R) + P(O∩R) = 0.3825 + 0.084 + 0.0246 + P(O∩R) → P(O∩R) = 0.8397 - 0.4911 = 0.3486 → P_O(R) = 0.3486 / 0.42 ≈ 0.834. 万能献血者 = O型且Rh阴性: P(O ∩ R̄) = P(O) × P(R̄|O) = 0.42 × (1 - 0.83) = 0.42 × 0.17 = 0.07145. a. X ~ B(100, 0.0714) b. P(X ≤ 7) ≈ 0.577(使用计算器) c. E(X) = 100 × 0.0714 = 7.14;Var(X) ≈ 100 × 0.0714 × 0.9286 ≈ 6.636. a. M_N 表示N个城市采样平均每城献血者人数 b. E(M_N) = 7.14 c. Var(M_N) = 6.63 / N d. 使用切比雪夫不等式求出 N ≥ 6766
第二题(6分)解析
A. 图像阅读:1. 切线T_A的斜率即为f'(1),由图像可知其为−1。2. 图像上函数图像C_f在区间]0, 3]上有两处切线水平,对应f'(x)=0的两个解。3. 在x=0.2处,图像在切线下方,说明f''(0.2)<0,函数为凹的。B. 函数研究:f(x) = x(2ln²x − 3lnx + 2)1. 解方程2X²−3X+2=0,Δ=−7<0,无实根,故f(x)>0,函数不与横轴相交。2. x→+∞时,f(x) ≈ x(lnx)² → +∞,因此f(x) → +∞;已知x→0时f(x) → 0。3a. f'(x)=2ln²x + lnx −1,f''(x)=1/x (4lnx + 1)3b. 拐点发生在f''(x)=0,即4lnx+1=0 → x=e^−1/4x<e^−1/4时f''<0,凹;x>e^−1/4时f''>0,凸;拐点横坐标为e^−1/43c. 因e > e^−1/4,故在[1,+∞[上,C_f 位于切线T_B之上。C. 面积计算:1. 切线T_B在点B(e,e)处,与斜率f'(e)=2结合,得y = 2x − e2. 使用分部积分计算∫xlnx dx,得结果为(e² + 1)/43. 记面积A = ∫[1,e] (f(x) − (2x − e)) dx 设∫x(lnx)² dx = (e² − 1)/4,∫xlnx dx = (e² + 1)/4 整理得A = (3e²/4) − e − 5/4
第三题(4分)解析
命题1:A = (−1, 0, 5),B = (3, 2, −1),AB向量为(4, 2, −6),命题所给向量为(−2, −1, 3),为AB的倍数。用B点加上该向量可得相应参数式,命题成立。→ 命题1为真。命题2:向量(5, −2, 1)是否为平面OAB的法向量?计算与OA = (−1, 0, 5)、OB = (3, 2, −1)的点积:- 与OA点积 = 0,但与OB点积 ≠ 0,说明不是同时垂直两个向量→ 命题2为假。命题3:d与d′的方向向量不共线。解方程判断是否有公共点:设k = −4,s = 2.5,代入三式后满足 → d与d′相交 ⇒ 共面。→ 命题3为假。命题4:点C(2, −1, 2)到平面P:x−y+z+1=0的距离:投影至法向量(1,−1,1)方向,距离 = √(2² + (−2)² + 2²) = √12 = 2√3→ 命题4为真。
第四题(5分)解析
A. 离散模型:1. u_1 = −0.02×1² + 1.3×1 = 1.28(公顷)2. 证明递增有界:- 设函数h(x)=−0.02x² + 1.3x,在[0,20]上递增 - 初值u_0=1,u_1=1.28 ≥ 1 - 假设对n成立,则u_{n+1}=h(u_n) ≥ h(1)=1.28,且 ≤ h(20)=18 → 由数学归纳法,得1≤u_n≤u_{n+1}≤203. (b) 由单调有界→收敛,设极限为L (c) 代入递推式L=−0.02L²+1.3L → 解得L=154. (a) 因为单调递增且极限大于14 → 一定存在某n使u_n>14 (b) 补全算法如下:def seuil(): n = 0 u = 1 while u <= 14: n += 1 u = -0.02*u**2 + 1.3*u return nB. 连续模型:1. 定义g(t) = 1/f(t),对g求导得g'(t) = −0.3g + 0.022. 解微分方程得通解:g(t) = Ce^(-0.3t) + 1/153. 整理f(t) = 1/g(t) = 15/(15Ce^(-0.3t) + 1),由f(0)=1解得C=14/15 得f(t) = 15/(14e^(-0.3t) + 1)4. 取极限:t→+∞时,f(t) → 155. 解不等式f(t)>14 → 解得t > ln(196)/0.3 ≈ 17.59 即2024年起18年后(约2042年),覆盖面积超过14公顷
⚠️声明:
本翻译稿为2025年法国高中毕业会考《数学专业(第一场)》大陆地区试卷的非官方中文翻译版本,仅供学习与参考之用。由于编辑与排版限制,原题中的图像(如函数图像、树状图等)与部分数学公式(如积分、导数、向量等)未在本文件中完全呈现,请务必对照原始试卷(法文原版PDF)进行查看与理解。
如对题意、图形或公式表达有疑问,建议参考原试卷内容,以确保准确无误地把握题目要求。