作为锚定特定资产价值(如法币、黄金等)的加密货币,稳定币凭借其价格稳定性与区块链技术的高效性,逐渐成为连接去中心化金融(DeFi)与传统金融体系的关键枢纽。
它不仅为加密货币市场提供流动性缓冲,更在跨境支付、供应链金融等领域开辟了低成本、高透明度的新路径。然而,长期缺乏明确监管的现状,使其系统性风险与合规隐患成为阻碍主流金融体系接纳的核心障碍。
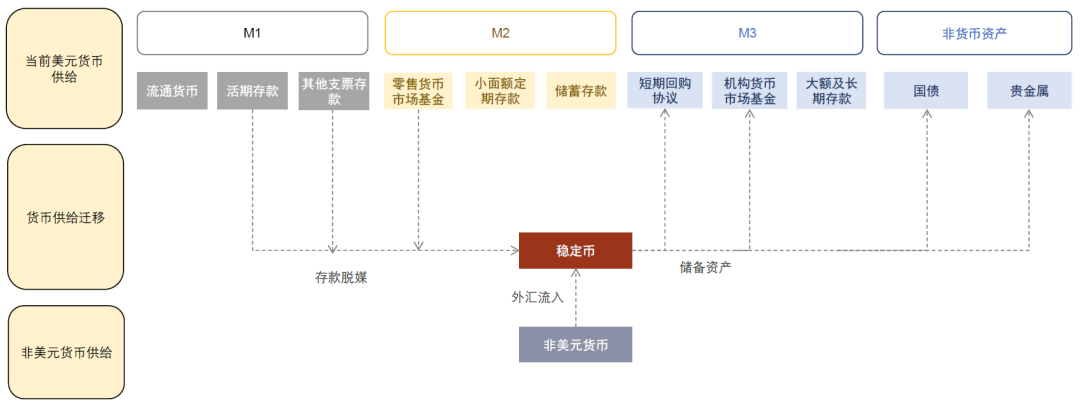
监管破局:美港框架树立合规里程碑
近期,美国与中国香港地区相继推出针对性监管框架,标志着稳定币正式步入规范化时代。
- 美国通过《支付稳定币法案》要求发行方需持银行牌照,并实施100%法币储备及月度审计,重点防范类似Terra/Luna的崩盘事件;
- 香港金管局颁布《稳定币发行人指引》,强调发行方需满足资本充足率、储备资产隔离及每日披露要求,并明确将港元稳定币纳入金融基础设施统筹。这两大经济体的政策设计均以“风险隔离”和“投资者保护”为底层逻辑,为传统机构安全进入加密市场扫除了合规障碍。
(图片来源于网络,如有侵权,请联系删除)
项目介绍
国外小组科研——致理计划:密集项目:量化金融与金融工程专题:金融衍生品、期权定价模型与量化交易策略研究---基于马尔可夫过程、伊藤引理、期权希腊值与波动率微笑下的期权估值与投资风险优化

本项目内容主要涵盖金融衍生品投资策略、期权定价模型、金融衍生品投资分析等复杂的金融投资策略和金融数学模型,重点讲授对当下投资决策产生重大影响的基础模型---二项式模型与BS模型。
布莱克-舒尔斯模型(英语:Black-Scholes Model),简称BS模型,是一种为金融衍生工具中的期权定价的数学模型,由美国经济学家迈伦·舒尔斯与费希尔·布莱克首先提出。此模型适用于没有派发股息的欧式期权。
罗伯特·C·墨顿其后修改了数学模型,使其于有派发股息时亦可使用,新模型被称为布莱克-舒尔斯-墨顿模型(英语:Black–Scholes–Merton model)。此模型的应用是透过买卖价格过高或是过低的期权,并同时与持有的资产对冲,来消除可能潜在的风险,并因此而套利。此方法也被称为“动态 Delta中性”。
此公式问世后带来了期权市场的繁荣,并且也是在投资银行与对冲基金中被广为使用的基础模型。同时导师也会阐述多个金融工程与金融数学中的高阶期权定价和策略模型。
这其中包括微笑曲线、Markov随机过程分析、伊藤引理、期权希腊值等。我们将更加强调实证金融(大量使用彭博专业数据)和上述科目的应用数学/量化分析方法来为学生更加深入的研究金融衍生品市场。
项目大纲
- 数字生态系统中的策略
- 产品业务如何与数字平台竞争
- 了解数字中断与数字转型
- 项目回顾与成果展示
- 论文辅导
教授介绍
导师:Alexei
学校:哥伦比亚大学 Columbia University
导师级别:正教授
专业方向:国际金融、金融管理、投资学、投资与理财
Alexei导师现任职于哥伦比亚大学,教授财务价格分析中的数学方法、资本市场和投资等课程,拥有普林斯顿大学应用与计算数学硕士及博士学位,是Systematic Alpha Management LLC (SAM)公司研究主管及合伙人。
导师研究成果广受业界认可,曾发表多篇论文于International Journal of Theoretical and Applied Finance、World Scientific等业内知名学术期刊中。Alexei教授目前是达索系统公司的物理开发高级专家和哥伦比亚大学数学系的兼职正教授。从2000年到2019年,他是Systematic Alpha Management, LLC的研究主管和投资组合经理。
在共同创立SAM之前,Alexei博士曾在Wexford Management(定量分析师,期权定价和交易)、BNP Paribas(专有交易员,全球固定收入期货定量交易)、TrendLogic Associates(研究助理总监,全球期货和股票策略)工作。在他的科学和金融职业生涯中,导师的很多工作成果被发表在主要的物理和金融期刊上。